I have worked with the mathematics of exterior ballistics for so long that I sometimes forget the general nature of the path of a rifle bullet to it’s target is not mind boggling obvious. I was reminded of this by an email I received today:
Need a answer: I was told that when shot a 30 cal. bullet goes up and makes an arc to the target, when held level. What happens, say at 100 yards.?
This email caused me to have a flashback to when I was in grade-school (yes Kris, firearms had been invented by the time I left grade-school).
When I was about the fourth grade a friend of mind, Verl (yeah, kids had strange names back in those days), insisted that the bullet would rise after it left the barrel of a rifle. I didn’t believe it and asked how long it took before it when into orbit (or some such thing that pointed out the absurdity of his claim). He didn’t know but asked his dad and came back to school and explained it went up for a while then came back down. My knowledge of and ability to articulate the physics of gravity and moving objects was limited and although I was profoundly unsatisfied with this explanation I couldn’t refute his assertion that it was true.
Later I made sense of it and eventually I wrote a computer programs that accurately predicts the path of a bullet as it leaves the muzzle. I am now much more capable of articulating the physics and will now attempt do so.
If you were to go to the range and instead of shooting the bullet you were to drop it from your fingers you would correctly expect the bullet to immediately accelerate toward the center of the earth and pick up speed at the rate of about 32 feet per second for each second it is in the air until it hit something. It doesn’t rise for a while then start falling. If you take a carpenter’s level to the range and line up the bore with the level such that the bore was horizontal and fire the gun the bullet will drop, relative to the horizontal, from the instant it leaves the barrel. It does not rise and then fall. It also does not fall at the same rate as a bullet you dropped from your fingers but that is another, much more complicated issue that is beyond the scope of this post.
Because the bullet immediately starts falling as it leaves the barrel in order for the sights to predict the impact point they are not aligned exactly parallel with the bore. They are aligned such that when you view the target they line up where the bullet will actually hit after bullet has dropped by whatever amount on it’s travel to the target. If the bore is horizontal the sights are pointed slight down. If the sights are horizontal then the bore will be pointed slightly up. In other words there is an angle between the line of sight and the bore of the gun. I call this angle the “Sight Angle”.
As far as I know I am the first to use the phrase “Sight Angle”. I use this to simplify the setting of the scope for long distance shooting. Most long range shooting instructors refer to your gun having a “Zero” that depends on the altitude, temperature, bullet velocity, and ballistic coefficient of the bullet. This is wrong. The gun is constant with respect to the environment. The drop of the bullet changes, not the scope setting.
Knowing the distance to the target and the drop the bullet makes when it goes this distance we can compute the proper angle the barrel should be with the horizontal to hit a target that is the same distance above the ground as the muzzle of the barrel. This angle is the proper angle required to have the gun exactly compensate for the drop of the bullet on it’s way to the target. This angle is not the sight angle because there is another complication–the height of the sight above (almost always but not necessarily) the bore. For a typical scoped rifle the line of sight through the scope is about 1.5 inches above the center of the bore. I call this the sight height. Using some trigonometry the sight height and proper angles can all be number crunched into a single number that you can dial into your scope such that for any give range and bullet drop you can dial your scope to the proper angle and you have precisely compensated for the drop of the bullet such that where you line the sights up that is where the bullet is going to go (minus bullet inaccuracy, wind drift, and shooter error). This “proper angle” is my Sight Angle. If you know what the environment is and you know the angle of the scope (and its height) relative to the bore you will know where the bullet will hit for any given range.
So, the email asked for what happens at 100 yards. Here are the graphs (generated with Modern Ballistics, which I wrote).
First the drop for a bullet fired with the bore of the gun horizontal. This is for a .308 Winchester shooting Federal match 168 grain bullets at “standard conditions” (59 F, sea level). Yes, I know this graph is confusing. It is not the path of the bullet. This is the distance the bullet has dropped as it traverses from the muzzle to the target. The drop increases the further it travels:
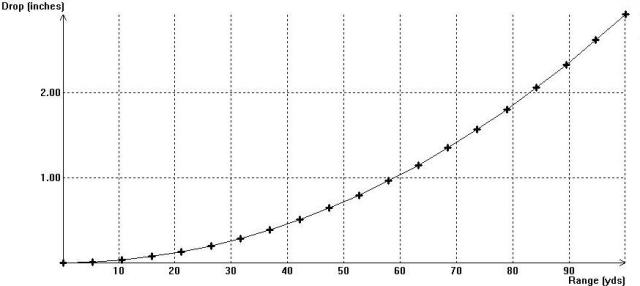
By the time the bullet has traveled 100 yards it has dropped nearly 3 inches. If you point the bore up at a slight angle (4.23 Minutes of Angle to be exact) compared to a scope mounted 1.5 inches above the center of the bore, aim the scope at a target 100 yards the bullet will start out 1.5 inches below the line of sight of the scope. Because the barrel is pointed up slightly as the bullet travels forward it will rise as it travels to the target. The distance from the line of sight through the scope to the bullet at any given range is called the height of the bullet at that range. Hence at the muzzle the height is -1.5 inches. And since the proper angle for a 100 yard zero was dialed into the scope the height at 100 yards will be 0.00 inches as seen in this graph:
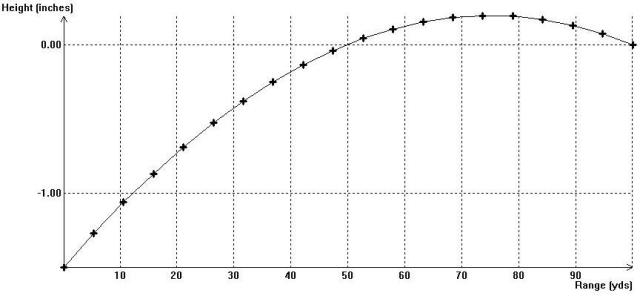
So, from the viewpoint of the scope the bullet does rise and then fall. Of particular interest is that there are actually two zeros for this scope setting. There is a “Near Zero” at 49.8 yards and there is the normal or “Far Zero” at 100 yards. At what is called the Midrange, 75.1 yards in this case, the bullet is at its maximum height of 0.2 inches above the line of sight.
So that is the path of the bullet for a 100 yard shot.
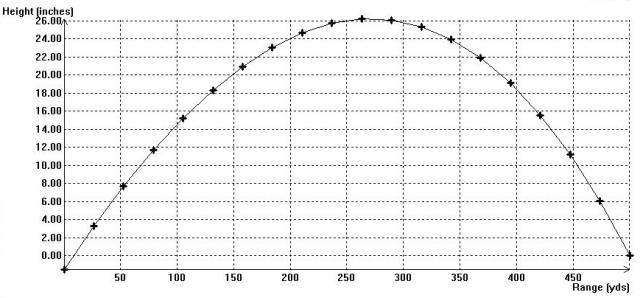
It is just my opinion but I don’t think shooting at 100 yards is very interesting with a rifle. The errors involved for temperature changes, air pressure, wind drift, and bullet velocity variations just don’t stack up enough to amount to much at that kind of range. For a .30 caliber rifle I don’t find things particularly interesting until we start shooting targets at 500 yards and beyond. I’m not going to get into all the interesting details because 99.9% of the people will find what I think is fascinating as mind bogglingly boring. But here is a hint of 500 yard shooting. A graph of the height of a bullet, again relative to the line of sight of the scope, for the same rifle and cartridge as above but for a 500 yard target:

I guess they were still using muzzle loading rifles back when you were in school :).
Excellent post. I very much like the way you explain this topic.
Ditto David, and I’ll take it further – I think that greater depth into this topic would be appreciated. I find it hard to internalize something unless I understand it, so this would actually greatly help me in learning to shoot well.
Don’t underestimate the nerdiness of your audience, Joe! 🙂
Greater depth appreciated – especially your hint as to why fall rates differ… argued about here
Also – so when sighting in for 100 yds, is there an easy way to tell if I’ve setup up to the near zero or far zero? I assume, for the 100yd example given, it involves shooting at the intermediate range of 75 yds to confirm it shoots 0.2″ high? For me, that would be hard to measure!
Dave thA
North Central Idaho
Beyond the Scope
“It also does not fall at the same rate as a bullet you dropped from your fingers but that is another, much more complicated issue that is beyond the scope of this post.”
To a first approximation, a horizontally fired bullet SHOULD (I think) fall at the same rate as a dropped one. Assume perfect vacuum, singular point bullet, no rotation, etc. The only forces are the horizontal force of the gun and the vertical force (acceleration) of gravity, which is the same vector for a stationary or moving bullet.
So, how does it work in the real world?
As I write, I’m thinking of an answer. Since the bullet takes a parabolic path, even in a vacuum, it starts to convert some of its horizontal velocity to vertical as it starts to point downward, adding to gravity’s acceleration. Maybe that’s it?
Bob K
In a vacuum, yes, it will fall at the same rate. It has to do with vertical terminal velocity being achieved via a component of the horizontal velocity. Hence it falls slower than the bullet dropped from your fingers.
It’s partially “in orbit” too. I mean, if you fire with a level barrel, the bullet is going off at a tangent to the curve of the Earth, and so it is initially rising, vacuum or no. Maybe you said that; “…vertical terminal velocity being achieved via a component of the horizontal velocity” but I can’t tell. Your words are strange to me. Then there’s the velocity of the Earth’s rotation varying with latitude, and the direction you’re firing relative to the direction of the Earth’s rotation. Those are pretty small factors, sure, but it is my understanding that long-range artillery gunners take them into consideration.
“How long…before it went into orbit?”
My smart-ass answer would be that it’s in orbit immediately. It’s just that the orbit is so highly eliptical that it intersects with the Earth’s surface very soon after launch ; )
Thanks. This explains something we did in boot camp. I think. At Parris Island we zeroed our rifles on a very short range before we went to the 200, 300, and 500 meter ranges. I think it was 21 feet but don’t hold me to that, it was 28 years ago. Anyway, would that be the near zero for the 5.56 NATO cartridge out of an M16?
Dave thA,
With nearly all configurations of ammo and scopes tough to get a near zero much past past 100 yards. With a high scope height (such as 2.6″ with AR-15 with iron sights) and the right ammo you can make them both 100 yards but that is about it. I’ll make another post about this sometime when my wife isn’t waiting for me.
Unless it makes one complete revolution around the earth I consider it suborbital.
For the purposes of small arms all that really matters is the deviation of the bullet from the line of sight through the scope or other sighting device. The curvature of the earth doesn’t enter into this.
When I was writing Modern Ballistics I calculated the effects of the earths rotation and, IIRC, for all of the continental U.S. the error at 1000 yards was less than 0.1 MOA for a 30.06 shooting a 168 grain Match King. Because this was much less than other errors such as wind estimation errors and it was difficult to determine and input the relevant data I decided to ignore the earth rotational effects.
Another way to look at the reason why the drop isn’t the same as a bullet dropped from your fingers is that the drag on the bullet at supersonic speeds causes it to slow down. If the bullet is going mostly horizontal with a small vertical component the drag in the vertical direction is becomes equal to the drag of terminal velocity much sooner than the bullet dropped from your fingers reaches terminal velocity.